TERMODINÂMICA DE GRACELI ONDE OCORREM VARIAÇÕES CONFORME O SISTEMA DE DIMENSÕES, CATEGORRIAS E ESTADOS DE GRACELI. PRESSENTE NO SDCTIE GRACELI.
Condução quântica[editar | editar código-fonte]
Segundo som é um fenômeno mecânico quântico no qual transferência de calor ocorre por movimento na forma de onda, em vez de pelo mecanismo mais comum da difusão. Calor toma o lugar da pressão nas ondas de som normais. Isto conduz a uma condutividade térmica muita alta. É conhecido como "segundo som" porque a onda de calor é similar à propagação de som no ar.
Lei de Fourier[editar | editar código-fonte]
A lei da condução térmica, também conhecida como lei de Fourier, estabelece que o fluxo de calor através de um material é proporcional ao gradiente negativo de temperatura. Podemos enunciar esta lei de duas formas equivalentes: a forma integral, em que olhamos para a quantidade de energia que flui para dentro ou para fora de um corpo como um todo; e a forma diferencial, em que olhamos para os fluxos de energia localmente. O fluxo de calor é a quantidade de energia que flui através de uma unidade de área por unidade de tempo.
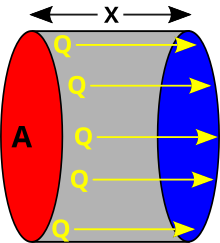
Pode-se determinar o fluxo de calor transportado por condução pela Lei de Fourier:
/ SDCTIE GRACELI.
A expressão acima aplica-se ao caso unidimensional, quando há gradiente de temperatura apenas na direção .
Se a distribuição de temperatura for linear e, neste caso , a equação acima toma a forma:
/ SDCTIE GRACELI.
A constante , é a condutividade térmica do material. Entre duas substâncias, a que tiver condutividade maior conseguirá transferir uma quantidade maior de calor, para uma mesma diferença de temperatura.
Teorização completa[editar | editar código-fonte]

Existem várias grandezas envolvidas, mas entre elas existem duas que são de muita importância de interesse prático no estudo de problemas de condução de calor. Estas grandezas são a razão de fluxo de calor e a distribuição da temperatura. As razões de fluxo de calor tratam da demanda de energia em um dado sistema, quando se requer uma distribuição de temperaturas conveniente para desenhar de maneira adequada no sistema, desde o ponto de vista dos materiais. Em um fenômeno qualquer, uma vez que seja conhecida a distribuição da temperatura é possível determinar as razões de fluxo de calor com ajuda da denominada Lei de Fourier (de 1822, estabelecida por Jean Baptiste Joseph Fourier).
A distribuição da temperatura é linear, e o fluxo de calor é constante de um extremo a outro de uma placa, para o caso da equação radial produzida.
E portanto a distribuição da temperatura apresenta-se em forma logarítmica:
/ SDCTIE GRACELI.
O calor transferido é tratado pela lei de Fourier que descreve especificamente previsões (modelagens) de comportamento para o caso simples de um corpo sólido, com duas paredes paralelas:[15][16]
/ SDCTIE GRACELI.
A unidade de é o Watt (), e sendo as grandezas:
- a temperatura da superfície da parede mais quente
- a temperatura da superfície da parede fria
- da área através da qual o calor flui,
- a condutividade térmica, geralmente um parâmetro do material dependente da temperatura, e
- a espessura do corpo, medido de parede a parede.
Atualmente a transferência de calor é descrita através do conceito mais rigoroso de fluxo de calor , em abordagens que visam reduzir-se aos tratamentos de Fourier e Newton. A notação é formulada a partir da derivada parcial no tempo do vetor fluxo de calor . Aplica-se a seguinte definição:
/ SDCTIE GRACELI.
Matematicamente, o fenômeno de "transferência de calor" é descrito por uma equação diferencial parcial, apresentando um padrão parabólico. Esta equação diferencial parcial, na forma especificada, apresenta a forma geral:
/ SDCTIE GRACELI.
Sendo esta equação especial e chamada comumente equação do calor. Note-se que esta forma da equação do calor é válida somente para meios homogêneos e isotrópicos; noutras palavras, para meios que possuem a mesma composição em todos os lugares e nenhuma orientação preferencial (ocorrem orientações preferenciais, por exemplo, em fibras de materiais compostos, mas também por dilatações de grãos em chapas de aço laminadas, etc). Para estes casos - e apenas para isso , as propriedades materiais são adotadas com o objetivo de considerar apenas as grandezas dependentes da temperatura. Estritamente falando, a equação assim formulada não se aplica apenas quando o calor no corpo é introduzido ou removido por fenômenos estranhos à modelagem utilizada, sendo, neste caso, a fonte ou "fuga" um termo a ser adicionado ao equacionamento. Com estas restrições, segue-se a seguinte forma da equação do calor:
/ SDCTIE GRACELI.
Sendo esta a equação diferencial que descreve os processos de transporte em geral (como o processo de difusão - que é um transporte material, devido a ser compreendido como uma diferença de concentração ou, no caso da equação do calor, apenas o "andar" da distribuição de temperatura em um corpo devido a um gradiente de temperatura). A solução analítica dessa equação não é em possível muitos casos práticos, sendo calculados, atualmente, com a ajuda de métodos tecnicamente relevantes de cálculos para fenômenos de transferência de calor como o método dos elementos finitos, obtendo-se como resultado a distribuição temporal da temperatura no espaço (um campo de temperaturas). Assim, pode-se obter influências, por exemplo, relacionadas ao comportamento de expansão espacial dos componentes (dilatação térmica), que por sua vez influenciará o estado de tensão local. Assim, o campo de temperaturas torna-se uma base importante para todas as tarefas de engenharia em que o componente de estresse térmico não pode ser negligenciado no projeto.
Forma diferencial[editar | editar código-fonte]
A forma diferencial da lei de Fourier da condução térmica mostra que o fluxo de calor local, , é igual ao produto da condutividade térmica, , e o gradiente de temperatura local negativo, . O fluxo de calor é a quantidade de energia que flui através de uma superfície particular por unidade de área por unidade de tempo.
/ SDCTIE GRACELI.
onde (incluindo as unidades SI)
- é o fluxo de calor local, [W·m−2]
- é a condutividade térmica do material, [W·m−1·K−1],
- é o gradiente de temperatura, [K·m−1].
A condutividade térmica, , é frequentemente tratada como um constante, embora isto nem sempre seja verdade. Enquanto a condutividade térmica de um material geralmente varia com a temperatura, a variação pode ser pequena para uma significativa faixa de temperaturas para alguns materiais comuns. Em materiais anisotrópicos, a condutividade térmica varia tipicamente com orientação; neste caso é representada por um tensor de segunda ordem. Em materiais não uniformes, varia com a localização espacial.
Para muitas aplicações simples, a lei de Fourier é usada em sua forma unidimensional. Na direção ,
/ SDCTIE GRACELI.
Forma integral[editar | editar código-fonte]
Pela integração da forma diferencial sobre a superfície total do material , chega-se à forma integral da lei de Fourier:
/ SDCTIE GRACELI.
onde (incluindo as unidades SI)
- é a quantidade de calor transferido por unidade de tempo e
- é um elemento de área de superfície orientado
A equação diferencial acima, quando integrada para um material homogêneo de geometria 1-D entre dois pontos a uma temperatura constante, dá a taxa de fluxo de calor como:
/ SDCTIE GRACELI.
onde
- é a área da superfície da seção transversal,
- é a diferença de temperatura entre os extremos,
- é a distância entre os extremos.
Esta lei forma a base para a derivação da equação do calor. A lei de Ohm é o análogo elétrico da lei de Fourier.
Condutância[editar | editar código-fonte]
Escrevendo-se
/ SDCTIE GRACELI.
onde é a condutância, em .
/ SDCTIE GRACELI.
Lei de Fourier pode também ser enunciada como:
/ SDCTIE GRACELI.
A recíproca da condutância é a resistência, , dada por:
/ SDCTIE GRACELI.
e é a resistência que é aditiva quando várias camadas condutivas situam-se entre as regiões quente e fria, porque e são as mesmas para todas as camadas. Em uma partição de multicamadas, a condutância total está relacionada com a condutância de suas camadas por:
/ SDCTIE GRACELI.
Assim, quando trata-se de uma partição de multicamadas, a seguinte fórmula é geralmente usada:
/ SDCTIE GRACELI.
Quando o calor é conduzido a partir de um fluido para outro através de uma barreira, às vezes é importante considerar a condutância da fina película de fluido que permanece estacionária próximo a barreira. Esta fina película de líquido é difícil de quantificar, suas características, dependendo das complexas de turbulência e viscosidade, mas quando se lida com os obstáculos finos de alta condutância por vezes pode ser bastante significativa.
Representação de propriedade intensiva[editar | editar código-fonte]
As equações de condutância anteriores escritas em termos de propriedades extensivas, podem ser reformuladas em termos de propriedades intensivas. Idealmente, as fórmulas de condutância devem produzir uma grandeza com dimensões independentes da distância, como a lei de Ohm da resistência elétrica:
- ,
/ SDCTIE GRACELI.
e a condutância:
- .
/ SDCTIE GRACELI.
A partir da fórmula elétrica:
- ,
/ SDCTIE GRACELI.
onde é a resistividade, é o comprimento e é a área de seção tranversal, temos
- ,
/ SDCTIE GRACELI.
onde é a condutância, é a condutividade, é o comprimento e é a área de seção tranversal.
Para o calor,
/ SDCTIE GRACELI.
onde é a condutância.
Lei de Fourier pode ser enunciada como:
/ SDCTIE GRACELI.
análoga a lei de Ohm:
- ou
/ SDCTIE GRACELI.
A recíproca da condutância é resistência, , dado por:
/ SDCTIE GRACELI.
análoga a lei de Ohm:
/ SDCTIE GRACELI.
A soma das condutâncias em série é ainda correta.
Cilindros[editar | editar código-fonte]
Condução através de cilindros pode ser calculada quando conhece-se variáveis tais como o raio interno , o raio externo , e o comprimento notado como .
A diferença de temperatura entre a parede interna e externa pode ser expressa como .
A área do fluxo de calor:
/ SDCTIE GRACELI.
Quando a equação de Fourier é aplicada:
/ SDCTIE GRACELI.
Rearranjando-se:
/ SDCTIE GRACELI.
Portanto, a taxa de transferência de calor é
/ SDCTIE GRACELI.
A resistência térmica é
/ SDCTIE GRACELI.
Tendo-se , onde sendo importante notar que este é o raio log médio.
Condução em regime estacionário[editar | editar código-fonte]
Define-se um regime estacionário (ou permanente), quando as temperaturas não dependem do tempo. A temperatura depende apenas da disposição do ponto em que as medidas são tomadas ao longo do tempo. Para o restante desta divisão deste artigo, assume-se como estabelecido um estado de equilíbrio.
Superfície plana simples[editar | editar código-fonte]
O material é um meio condutor térmico delimitado por dois planos paralelos (o caso de uma parede). Cada plano tem uma temperatura homogênea por toda a sua superfície. Consideramos que os planos têm duas dimensões infinitas para superar os efeitos de borda. Por conseguinte, o fluxo de entrada é igual ao de saída, não há perda de calor nas extremidades.
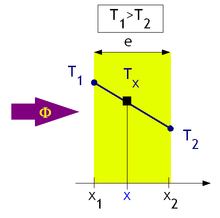
Note-se que a temperatura do plano situado na abscissa , e a temperatura do plano situado na abscissa . Note-se que é a espessura da parede. Em regime estacionário, é uma função linear de , assim:
/ SDCTIE GRACELI.
A densidade de fluxo de calor da superfície é escrita como:
- .
/ SDCTIE GRACELI.
O fluxo de calor através de uma superfície é:
/ SDCTIE GRACELI.
ou
/ SDCTIE GRACELI.

Analogia elétrica
Por analogia com a eletricidade (lei de Ohm) no caso especial onde a área de contato entre cada material é constante (fluxo superficial constante), podemos traçar um paralelo entre as duas expressões:
/ SDCTIE GRACELI.
Pode-se traçar um paralelo da primeira com a tensão e a temperatura, da outra parte a intensidade e o fluxo de calor:
/ SDCTIE GRACELI.
Pode-se então definir uma resistência térmica, desempenhando a transferência de calor um papel semelhante ao da resistência elétrica.
/ SDCTIE GRACELI.
onde é a superfície do material e a espessura. A resistência térmica é homogênea e expressa em .
Surperfícies planas em série[editar | editar código-fonte]
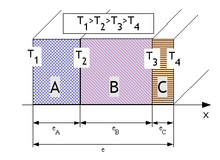
Considere-se materiais A,B e C de espessura respectivamente , e e de condutividade térmica respetivamente , e .
Os pressupostos são idênticos aos de uma única superfície plana. Consideramos que o contacto entre cada camada é perfeito, o que significa que a temperatura na interface entre dois materiais é idêntica em cada material (temperatura não salta na passagem por uma interface).
Finalmente, a área de contato entre cada material é constante, o que implica um fluxo de superfície constante.
As resistências térmicas se adicionam:
/ SDCTIE GRACELI.
Demonstração[editar | editar código-fonte]
Globalmente, tem-se
/ SDCTIE GRACELI.
Se decomposto
- para a camada :
- para a camada :
- para a camada :
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
Nota: Dadas as hipóteses, o fluxo (ou a densidade de fluxo) permanece constante.
Com:
Portanto
/ SDCTIE GRACELI.
O perfil de temperaturas
Para cada material a variação da temperatura segue uma lei do tipo:
/ SDCTIE GRACELI.
A variação de temperatura é linear na espessura do material considerado. A inclinação é inversamente proporcional a (condutividade térmica) característica de cada material. Quanto maior a condutividade térmica e menor o material (e, portanto, menor o isolamento), menor será a inclinação.

Analogia elétrica
Da mesma forma que as resistências elétricas em série são adicionadas, as resistências térmicas em série são somadas.

Superfícies planas em paralelo[editar | editar código-fonte]

Considere-se materiais planos justapostos lado a lado. Cada material é homogêneo e delimitado por dois planos paralelos. Este poderia ser o modelo de uma parede com uma janela. As hipóteses são idênticas as de uma superfície plana única. Além disso, considera-se que a temperatura da superfície é uniforme em cada elemento ( et ). Considere-se as respectivas superfícies dos elementos .
Posteriormente, presume-se que o fluxo seja sempre perpendicular à parede composta; o que não é realista porque a temperatura da superfície de cada elemento da composição é diferente e há, portanto, um gradiente de temperatura lateral (a origem das pontes térmicas). Além disso, é necessário corrigir o fluxo de calor calculado na parede feita com os coeficientes de perda por unidade de comprimento, específicos para cada ramo de parede (e pode ser insignificante, cf. a regulamentação térmica RT 2000[17]).
As condutâncias térmicas se adicionam:
/ SDCTIE GRACELI.
Demonstração[editar | editar código-fonte]
Para cada elemento , o fluxo é expresso em função da relação
/ SDCTIE GRACELI.
Tendo-se em conta a analogia elétrica
/ SDCTIE GRACELI.
como é igual a , ou
Tem-se, portanto
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
O fluxo total é igual à soma dos fluxos em cada elemento
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
Sendo a surperfície total
/ SDCTIE GRACELI.
O fluxo na superfície é então
/ SDCTIE GRACELI.
Mais uma vez, por analogia com as leis elétricas, o inverso da resistência térmica é às vezes chamado condutividade térmica.
/ SDCTIE GRACELI.
Analogia elétrica
Também é possível fazer uma analogia entre um circuito elétrico de resistências em paralelo.
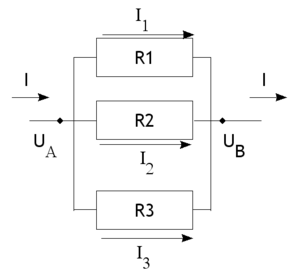 |  |
/ SDCTIE GRACELI. |
Superfície cilíndrica simples[editar | editar código-fonte]

O tubo simples consiste de um material único e homogêneo. A temperatura é uniforme em cada superfície do tubo. Considera-se o tubo infinitamente longo para superar os efeitos da borda.
A variação de temperatura é escrito:
/ SDCTIE GRACELI.
Demonstração[editar | editar código-fonte]
Considera-se uma variação dentro do material constituinte do tubo, a lei de Fourier é então expressa como:
/ SDCTIE GRACELI.
Variação da temperatura na espessura do tubo

Sendo a superfície de um cilindro:
/ SDCTIE GRACELI.
Podemos escrever a lei de Fourier na forma:
/ SDCTIE GRACELI.
A variação de temperatura no material é
/ SDCTIE GRACELI.
Em toda a espessura do tubo, a variação é
/ SDCTIE GRACELI.
Superfícies cilíndricas concêntricas[editar | editar código-fonte]

O tubo concêntrico é composto por tubos dispostos em camadas concêntricas. Considere-se que o contato é perfeito entre os tubos. A temperatura é uniforme em cada superfície do tubo. Considere-se que o tubo possui um comprimento interminável L para superar os efeitos de borda.
A resistência total do tubo é expressa por uma lei da tipo "série como a parede compondo uma série:
/ SDCTIE GRACELI.
Demonstração[editar | editar código-fonte]
Evolução da temperatura na primeira camada:
/ SDCTIE GRACELI.
Evolução da temperatura na segunda camada:
/ SDCTIE GRACELI.
Em toda a espessura do tubo:
/ SDCTIE GRACELI.
A resistência térmica da camada
/ SDCTIE GRACELI.
A resistência térmica da camada
/ SDCTIE GRACELI.
Chegando-se a que resistência total do tubo é expressa por uma lei da tipo "série como a parede compondo uma série:
/ SDCTIE GRACELI.
Condução em regime dinâmico[editar | editar código-fonte]
A resolução da equação do calor em regime dinâmico é muito mais difícil. Ela usa os conceitos de transformada de Fourier de produto de convolução e distribuições. Apresentam-se alguns exemplos de resolução.
Caso de uma área ilimitado[editar | editar código-fonte]
Princípio geral[editar | editar código-fonte]
Escreve-se a equação do calor na forma:
/ SDCTIE GRACELI.
onde é o coeficiente de difusividade térmica e representa as fontes de calor. pode ser uma função do tempo e da posição da fonte de calor, mas também uma distribuição. Por exemplo, a injeção instantânea e pontual de uma quantidade de calor pode ser representada pelo produto de uma distribuição de Dirac no instante por uma distribuição de Dirac em é a abscissa em caso de problema unidimensional ou vetor de posição no caso geral.
Ela também dará o estado inicial do área , que também pode ser uma função de ou uma distribuição. Considera-se que é nulo para .
O método de solução consiste em:[18] [19]
- Aplica-se uma transformada de Fourier sobre a variável , a todos os termos da equação diferencial. Isto transforma a derivação com relação a em um produto. Toma-se , então a equação torna-se:
/ SDCTIE GRACELI.
ou melhor, no sentido de distribuições:
/ SDCTIE GRACELI.
tendo-se em conta a condição inicial.
- Reconhecendo-se nesta equação um produto de convolução:
/ SDCTIE GRACELI.
O operador aplicado a é um produto de convolução relativo à variável .
- Aplicando o operador inverso, prova-se que , onde é a função de Heaviside, conduzindo a:
/ SDCTIE GRACELI.
Se é uma função e não uma distribuição, esta relação se torna, para :
/ SDCTIE GRACELI.
- Toma-se a transformada de Fourier inversa para deduzir .
Caso particular[editar | editar código-fonte]

Toma-se em (injeção instantânea de calor em um determinado ponto), o método acima descrito conduz a:
/ SDCTIE GRACELI.
Assim, para :
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
cuja transformada de Fourier inversa é, para :
- no caso unidimensional.
- no caso tridimensional.
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
Área ilimitado sem fonte de calor[editar | editar código-fonte]
Se toma-se somente a temperatura inicial de uma fonte média independente de calor (), tem-se que:
- no caso unidimensional.
- no caso tridimensional.
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
Caso de áreas limitadas, sem fonte de calor[editar | editar código-fonte]
Caso de uma área limitada por um plano. O problema de Kelvin[editar | editar código-fonte]

Supondo-se o área limitada pelo plano . Se coloca-se por condição os limites suplementares para todo , então basta estender a distribuição inicial de temperatura por uma função ímpar em e aplicar-se o resultado anterior.
O caso mais célebre é o problema de Kelvin. Este considerou em 1860 que a Terra estava inicialmente a uma temperatura constante da ordem de 3000° e que se resfriava por simples condução. Utilizando o valor atual do gradiente de temperatura em função da profundidade, ele deduziu uma estimativa para a idade da Terra. Pode-se aplicar o método de resolução acima para considerar a Terra como plana e infinitamente profunda, delimitado por um plano de sua superfície. O cálculo conduz a:
/ SDCTIE GRACELI.
onde é chamada função erro de Gauss.
O gradiente de temperatura na superfície será:
/ SDCTIE GRACELI.
Conhecendo-se como sendo da ordem de 3 °C para cada 100 metros de profundidade e estimado como , obtem-se que t vale 100 milhões de anos. Este resultado é largamente subestimado pois Kelvin ignora os fenômenos de convecção no interior do manto terrestre.[20] [21]
Caso de uma área limitada por dois planos paralelos[editar | editar código-fonte]

Considere-se uma área limitada por dois planos e . Supondo-se que são dadas como condições de contorno os limites . Utiliza-se um método de resolução baseado nas séries de Fourier, procurando-se sob a forma:
/ SDCTIE GRACELI.
Esta expressão verifica tanto a equação do calor quanto as condições de contorno nos limites. Se é tomada a distribuição de temperatura inicial , é suficiente expandir-se em uma série de Fourier para determinar-se os coeficientes .
Por exemplo, se tiver-se constante, obtem-se:
/ SDCTIE GRACELI.
Ao deixar-se L ao infinito, encontra-se a solução de Kelvin do parágrafo anterior, a soma acima é considerado uma soma de Riemann convergindo para a integral.
Caso de uma área de geometria esférica[editar | editar código-fonte]

Se o caso de propagação se sá em uma área esférica, e onde a temperatura não depede apenas das distância ao centro, a equação de calor torna-se a expressão do laplaciano em uma esfera:
/ SDCTIE GRACELI.
Se coloca-se , a equação torna-se:
/ SDCTIE GRACELI.
Podemos, então, aplicar os métodos anteriores para determinar , então deduzir dividindo por .
Assim, resolvendo-se o problema de Kelvin, no caso de uma esfera de raio (temperatura inicial uniforme igual à ,a superfície é mantida a uma temperatura igual a zero) conduz à seguinte expressão para :
/ SDCTIE GRACELI.
onde é a função sinus cardinal.
Caso de áreas limitadas, com fonte de calor[editar | editar código-fonte]
Considere-se a equação:
/ SDCTIE GRACELI.
com não nulo. Em geral, procura-se uma solução particular para esta equação, de modo que, uma vez relacionada a , pode ser reduzida a uma equação sem segundo membro. Apresentam-se alguns exemplos, onde representa uma densidade de fonte de calor constante, independente da posição e do tempo.
Área limitada por dois planos paralelos[editar | editar código-fonte]

Considere-se uma área limitada pelos dois planos e . Supondo-se que no momento inicial, a temperatura da área é igual a uma temperaturea de referência nula, e que as bordas da área se manterão permanentemente esta temperatura nula. satisfaz, pois:
- para todo positivo.
- para todo entre e .
/ SDCTIE GRACELI.
A função independente de satisfaz as duas primeiras relações, de maneira que coloca-se que ,
/ SDCTIE GRACELI.
então satisfaz:
/ SDCTIE GRACELI.
Pode-se aplicar o método visto acima na busca de sob a forma de uma série:
/ SDCTIE GRACELI.
que satisfaça as duas primeiras relações. Dado que, por razões de simetria, é esperado que , pode-se supor que os coeficientes sejam nulos quando é par, de maneira que:
/ SDCTIE GRACELI.
Para , tem-se:
/ SDCTIE GRACELI.
Obtem-se em desenvolver-se em série de Fourier. Encontrando-se:
/ SDCTIE GRACELI.
Assim , finalmente:
/ SDCTIE GRACELI.
Quando tende ao infinito, a temperatura da área tende a , o aquecimento tende a se equilibrar com a perda de calor pelas duas bordas.
Área limitada por um plano[editar | editar código-fonte]

A resolução do mesmo problema do caso em que consiste em determinar tal que:
- para todo positivo.
- para todo .
/ SDCTIE GRACELI.
Pode ser obter a solução deixando infinito na expressão dada no parágrafo anterior, igualando a série a uma soma de Riemann. Isto resulta na seguinte expressão:
/ SDCTIE GRACELI.
é a função chamada função erro de Gauss. Pode-se também encontrar esta expressão pela aplicação do método derivado do princípio geral relativo a uma área ilimitada, depois de estender a todo o espaço as funções em duas funções ímpares em , de modo que se anula em .
Quando tende ao infinito, é de cerca de , análogo aquela de uma área infinita. A borda única não é suficiente para dissipar o calor.
Área de uma geometria esférica[editar | editar código-fonte]

Dado o caso de uma área cuja borda seja uma esfera de raio , utiliza-se a expressão do Laplaciano em esfera e tem-se de resolver:
- Para todo
- Para todo
/ SDCTIE GRACELI.
Pergunta-se se ,
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
satisfaz o sistema:
- Para todo
- Para todo
/ SDCTIE GRACELI.
/ SDCTIE GRACELI.
O método das séries de Fourier sugere a busca de sob a forma de uma série ,
/ SDCTIE GRACELI.
onde os coeficientes encontram-se em desenvolvimento em série de Fourier. Obtendo-se:
/ SDCTIE GRACELI.
e, portanto:
/ SDCTIE GRACELI.
onde é a função sinus cardinal.
Quando tende ao infinito, a temperatura tende à distribuição limite . /




























![{\displaystyle [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53adac4d38fc744470f0d0f79113e1c05d9e8564)

![{\displaystyle [m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69984844e55299dd28db0ef5e3478d6395f4514e)





























































































































































































Comentários
Postar um comentário